ピンホール写真の数学
概要
第一稿.
, グラフの画質向上.
, 表記の改良.
グラフの誤り訂正.
等光像面の近似式を更新.
, . 「像面上の減光量」追加.
. 「厚みによるケラレと光束の歪み」を全部修正.
, . 「像面上の減光量」追記.
ピンホールカメラとは、板に穴を空けただけで写真を撮る、極めて原始的なカメラである。撮れる像は普段目にする写真と比べるとぼやけているのだが、そこがむしろ絵画における印象派のようで、写実ではなく芸術として興味深い表現方法の一つになっている。
ちなみに、似たような名前であるがスパイ用のカメラはピンホールレンズという小さなレンズが付いているが、ピンホールカメラにはレンズが付かない。
一般的なレンズによる写真と比べてピンホール写真が際立つ点の一つとして、露光時間が必然的に長時間露光になる点がある。このため撮影対象やフレーミングなど、普段より撮影の手順を意識するようになる。これにより撮れる像も時間の経過を感じさせるものとなるため、その結像の甘さに代えても魅力的な写真となる可能性を秘めているのである。
二点目として、自らがかなりの自由度で設計できるため、一般的なレンズを用いると高額になってしまう超広角撮影を手頃に楽しめる点がある。ダイナミックな構図で写真を撮りたいのであれば、ピンホールカメラは一考の余地があるのではないだろうか。
また、レンズのある写真と比べて被写界深度が非常に深いため、極端なクローズアップ撮影が可能なのも魅力の一つである。ピンホールカメラの目の前に対象を置き、思った通りの写真が出来上がった時の喜びはひとしおである。
また、レンズによる複雑な計算を必要とせず、必要な値は全て手計算で求まる点も、その像とは別の意味で興味深いと言えるだろう。
このページでは、いかに高品質な写真を撮れるピンホールカメラを設計できるかを念頭に、各種計算式やその結果などを示す。これからピンホールカメラを作ろうとしている方や、その数学的背景を知りたい方にとって、納得のいく情報を提示できれば幸いである。
点の像 X の大きさ
ある点を、直径 \(d\) のピンホールカメラで写すとき、その像 \(X\) の直径を求める。ある点からピンホールの中央までの距離を \(s\), ピンホール中央から像面までの距離を\(f\) とする。
三角形の相似より
\[ \begin{aligned} \frac{d/2}{s} &= \frac{X/2}{s+f}. \end{aligned} \] よって \[ \begin{aligned} X &= d \left( 1+ \frac{f}{s} \right) \\ &= d \left( 1+ M \right). \end{aligned} \]
ただし \(M = f/s\) は拡大率(マクロ比)である。ピンホール写真の場合、一般的には \(M = 0\) つまり無限遠で最適化させる。
エアリーディスクの大きさ
点光源からピンホールに入射した光は回折を起こし、中央の明るい円部分と周囲の輪状の縞部分とに分かれる。前者をエアリーディスク、後者をエアリーパターンと呼ぶ。エアリーパターンはエアリーディスクと比べて十分暗い。この時のエアリーディスクの直径を \(x\), 波長を \(\lambda\), ピンホールからエアリーディスクをなす角を \(\theta\) とすると、
\[ \begin{aligned} \sin\theta = 1.22 \frac{\lambda}{d}. \end{aligned} \] \(\theta \ll 1\) より \(\sin\theta \approx \tan\theta\) なので、
\[ \begin{aligned} \sin\theta &= 1.22 \frac{\lambda}{d} \\ &\approx \tan\theta = \frac{x/2}{f}. \\ \therefore x &\approx 2.44\lambda f/d \\ &=2.44\lambda \cdot F _{/\#}. \end{aligned} \]
ただし \(F _{/\#} = f/d\) は 口径比である。
また、式より \(x \propto 1/d \) なので、 \(x\) を小さくするためには \(d\) を大きくしなければならない。だがこれは \(X = d(1+M)\) と矛盾する。
最適なピンホールの大きさ
- https://www.youtube.com/watch?v=n5W3qztO4os
- https://www.diyphotography.net/the-comprehensive-tech-guide-to-pinhole-photography/
点光源の幾何学的像を \(B_G (=X)\), 点光源のエアリーディスクを \(B_D (=x)\) とし、これらを足したもの \(B\) を考える。この時、 \(d\) を変化させて \(B\) が最小となるような \(d\) を求める。
\[ \begin{aligned} B &= B_G + B_D \\ &= d(1+M) + 2.44\lambda f/d. \\ \end{aligned} \]
\(B\) を \(d\) で偏微分すると、 \[ \begin{aligned} \frac{\partial B}{\partial d} &= (1+M) - 2.44 \lambda f / d^2 \\ &= 0. \quad (\text{minimum of }B) \\ \therefore d &= \sqrt{\frac{2.44\lambda f}{1+M}}. \end{aligned} \]
このような \(d\) のときにこそ、最も尖鋭な像が得られる1。ここで、波長は可視光の平均値である緑色光の 555 [nm] = 0.000555 [mm] を用いるとする。なお、 \(M\) は大きくなるほど必要なピンホール径は小さくなる。
| \(f\) [mm] | 6 | 10 | 12 | 16 | 24 | 35 | 50 | 70 | 90 | 135 | 150 | 200 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(d\) [mm] | 0.0901 | 0.1164 | 0.1275 | 0.1472 | 0.1803 | 0.2177 | 0.2602 | 0.3079 | 0.3491 | 0.4276 | 0.4507 | 0.5204 |
画角
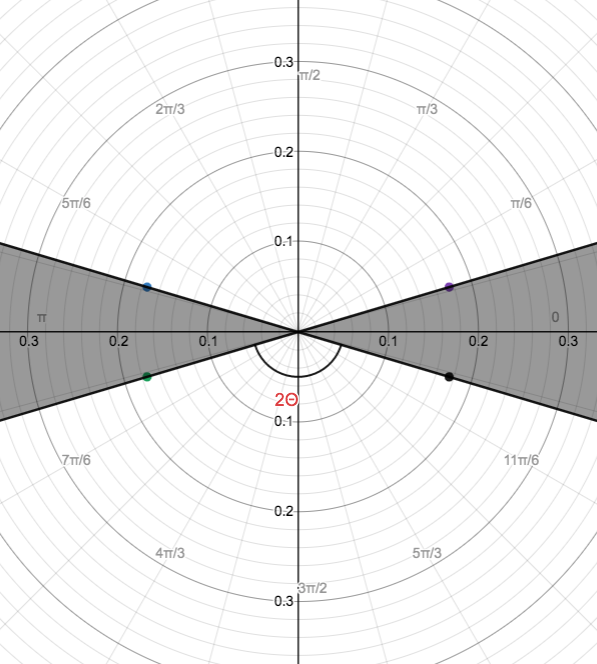
厚さ \(t\), 直径 \(d\) の穴をがなす角(イメージサークル)を \(2\Theta\) とすると、
\[ \begin{aligned} \tan \Theta &= d/t \\ 2\Theta &= 2 \tan ^{-1} (d/t). \end{aligned} \]
| \(f\) [mm] | \(d\) [mm] | \(2\Theta _{t=0.1}[°]\) | \(2\Theta _{t=0.05}[°]\) | \(2\Theta _{t=0.02}[°]\) | \(2\Theta _{t=0.01}[°]\) |
|---|---|---|---|---|---|
| 6 | 0.0901 | 84.04 | 121.94 | 154.97 | 167.33 |
| 10 | 0.1164 | 98.67 | 133.51 | 160.50 | 170.18 |
| 12 | 0.1275 | 103.78 | 137.17 | 162.17 | 171.03 |
| 16 | 0.1472 | 111.62 | 142.48 | 164.53 | 172.23 |
| 24 | 0.1803 | 121.97 | 149.00 | 167.34 | 173.65 |
| 35 | 0.2177 | 130.66 | 154.13 | 169.50 | 174.74 |
| 50 | 0.2602 | 137.95 | 158.25 | 171.21 | 175.60 |
| 70 | 0.3079 | 144.01 | 161.55 | 172.57 | 176.28 |
| 90 | 0.3491 | 148.03 | 163.70 | 173.44 | 176.72 |
| 135 | 0.4276 | 153.67 | 166.66 | 174.64 | 177.32 |
| 150 | 0.4507 | 154.98 | 167.34 | 174.92 | 177.46 |
| 200 | 0.5204 | 158.25 | 169.02 | 175.60 | 177.80 |
\(t\) の大きさはピンホール自体の強度や加工のしやすさに関わってくるので、必要なイメージサークルを与える \(t\) のうち最大のものを選びたい。一方、後ほど考察するが、周辺光量落ちをなるべく小さくするためには極力小さな \(t\) でなければならない。実際の製作において頭を悩ませる要素の一つになるだろう。
また、像平面の対角線 \(l\) , 焦点距離 \(f\) になす角を \(2\Phi\) とすると、
\[ \begin{aligned} \tan \Phi &= \frac{l/2}{f} \\ 2\Phi &= 2 \tan ^{-1} \left( \frac{l}{2f} \right). \end{aligned} \]
| image plane | 24x36 (35mm) | 24x54 (35mm x1.5) | 56x44 (6x4.5) | 24x72 (35mm x2) | 56x56 (6x6) | 56x88 (6x9) | 56x118 (6x12) | 56x168 (6x17) |
|---|---|---|---|---|---|---|---|---|
| \(f\) [mm] | \(2\Phi _{l=43} [°]\) | \(2\Phi _{l=59} [°]\) | \(2\Phi _{l=71} [°]\) | \(2\Phi _{l=76} [°]\) | \(2\Phi _{l=79} [°]\) | \(2\Phi _{l=103} [°]\) | \(2\Phi _{l=131} [°]\) | \(2\Phi _{l=175} [°]\) |
| 6 | 148.81 | 157.01 | 160.81 | 162.05 | 162.73 | 166.71 | 169.53 | 172.15 |
| 10 | 130.11 | 142.55 | 148.54 | 150.51 | 151.59 | 158.02 | 162.64 | 166.96 |
| 12 | 121.66 | 135.73 | 142.65 | 144.95 | 146.20 | 153.77 | 159.24 | 164.38 |
| 16 | 106.69 | 123.05 | 131.48 | 134.33 | 135.90 | 145.48 | 152.55 | 159.28 |
| 24 | 83.71 | 101.74 | 111.88 | 115.45 | 117.43 | 130.03 | 139.75 | 149.32 |
| 35 | 63.12 | 80.25 | 90.81 | 94.71 | 96.91 | 111.60 | 123.76 | 136.40 |
| 50 | 46.54 | 61.08 | 70.75 | 74.47 | 76.62 | 91.69 | 105.29 | 120.51 |
| 70 | 34.15 | 45.70 | 53.78 | 56.99 | 58.87 | 72.68 | 86.20 | 102.68 |
| 90 | 26.87 | 36.30 | 43.05 | 45.78 | 47.39 | 59.56 | 72.09 | 88.39 |
| 135 | 18.10 | 24.65 | 29.47 | 31.44 | 32.62 | 41.76 | 51.76 | 65.90 |
| 150 | 16.31 | 22.25 | 26.63 | 28.43 | 29.51 | 37.90 | 47.18 | 60.51 |
| 200 | 12.27 | 16.78 | 20.13 | 21.52 | 22.34 | 28.88 | 36.27 | 47.26 |
\(\Theta, \Phi\) の関係について考える。
- 像面が影にならない最小の \(\Theta\) は \(\Theta = \Phi\)
- 実際には余裕を見るため \(\Theta \gt \Phi\)
- 像面にビネットが生じない最小の \(\Theta\) は?
周辺光量落ち
上記のサイトにも図付きで詳しく説明されているが、ここでも同様に解説する。減光の要因について、コサイン誤差・光束断面の歪み・厚みによるケラレであると説明しているが、ここではコサイン誤差を最後に紹介する。
厚みによるケラレと光束の歪み
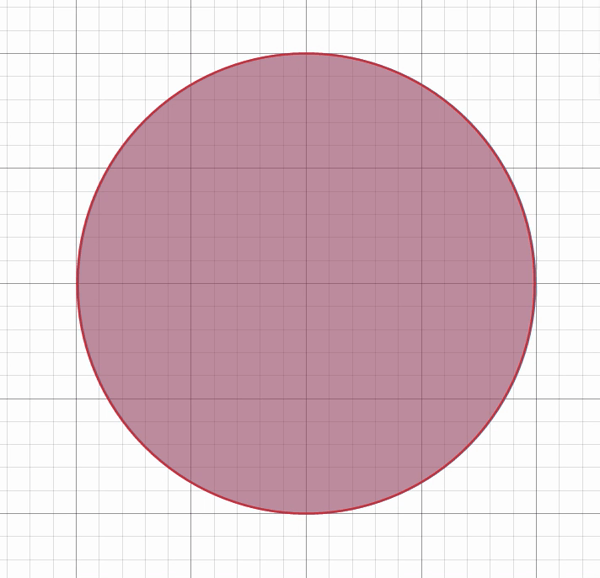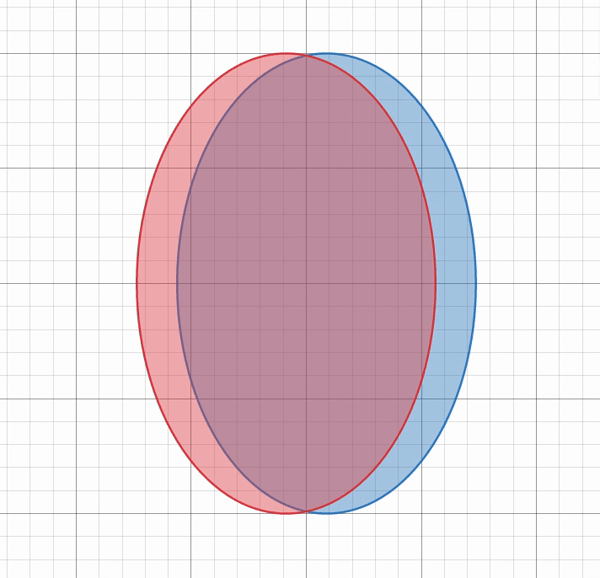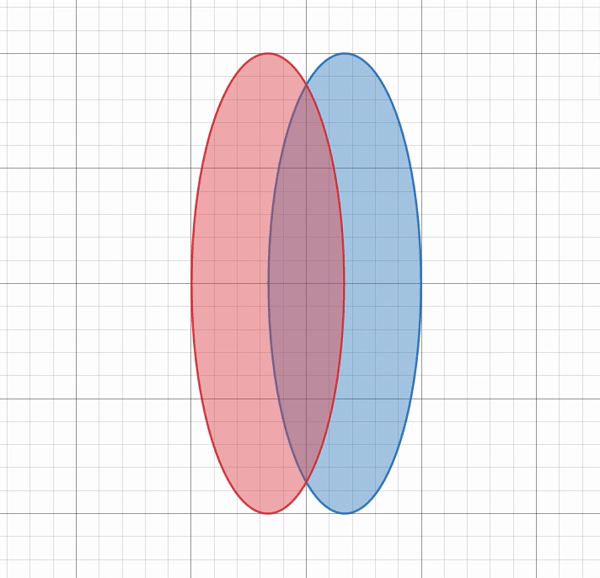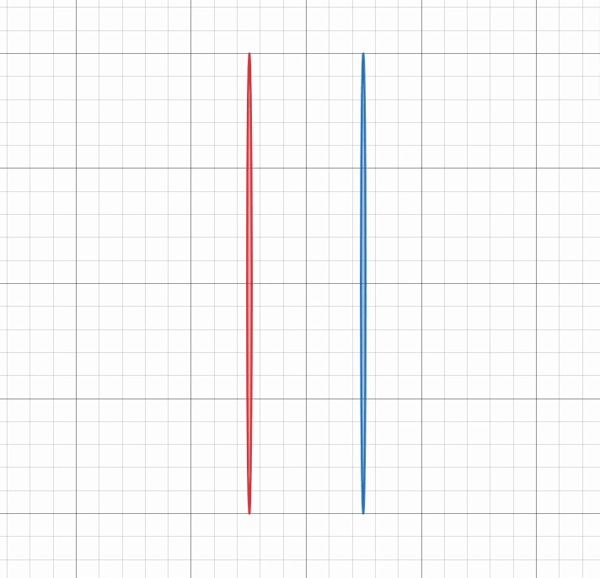
上の図のような厚さのある穴は、横から見た時に前面(被写体側)と後面(フィルム側)の円が重なる部分しか光を通さない。このように角度をつけて見ると、円は楕円に見える。ここでは以下のような条件で透過光の面積を求める。
\[t \lt d \ll f.\]
焦点距離 \(f\) はピンホールから十分離れている為、ピンホールの前面と後面の円の大きさは同じであると見做せる。
ピンホールの縁は全部で 4 箇所ある。それは前面の左 \(p_{\mathrm{FL}}\) と右 \(p_{\mathrm{FR}}\) 、後面の左 \(p_{\mathrm{BL}}\) と右 \(p_{\mathrm{BR}}\) である。これらの点を十分離れた所から角度 \(\theta\) をつけながら見るので、各点 \(p\) は \(\theta\) の関数であり、原点を見る視角と直交する直線上を通るように見える。つまり、次の図の各点を x 軸上に降ろしたように見える(なので \(\theta=0, \pi/2\) では前後の点が重なって見える)。
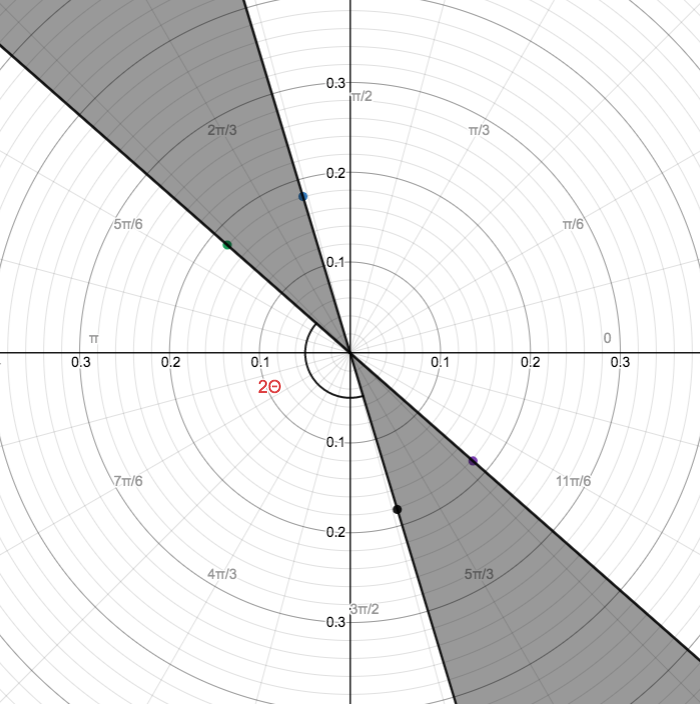
よって各点 \(p\) の関数は以下の通り:
\[ \begin{aligned} p_{\mathrm{FL}}(\theta) &= \sqrt{\left(\frac{d}{2} \right)^2 + \left(\frac{t}{2} \right)^2} \cos\left( \frac{\pi}{2} + \Theta - \theta \right), \\ p_{\mathrm{FR}}(\theta) &= \sqrt{\left(\frac{d}{2} \right)^2 + \left(\frac{t}{2} \right)^2} \cos\left( \frac{\pi}{2} - \Theta - \theta \right), \\ p_{\mathrm{BL}}(\theta) &= \sqrt{\left(\frac{d}{2} \right)^2 + \left(\frac{t}{2} \right)^2} \cos\left(-\frac{\pi}{2} - \Theta - \theta \right), \\ p_{\mathrm{BR}}(\theta) &= \sqrt{\left(\frac{d}{2} \right)^2 + \left(\frac{t}{2} \right)^2} \cos\left(-\frac{\pi}{2} + \Theta - \theta \right). \end{aligned} \]
ただし \(\Theta = \tan ^{-1} (d/t).\) この時前面の楕円と後面の楕円の式はそれぞれ次のように書ける。
\[ \begin{aligned} \frac{(x - p_{\mathrm{FL}}(\theta))(x - p_{\mathrm{FR}}(\theta))}{(p_{\mathrm{FR}}(\theta) - p_{\mathrm{FL}}(\theta))^{2}} + \frac{y^{2}}{d^{2}} &= 0, \\ \frac{(x - p_{\mathrm{BL}}(\theta))(x - p_{\mathrm{BR}}(\theta))}{(p_{\mathrm{BR}}(\theta) - p_{\mathrm{BL}}(\theta))^{2}} + \frac{y^{2}}{d^{2}} &= 0. \end{aligned} \]
この 2 楕円が重なる部分の面積を求める。
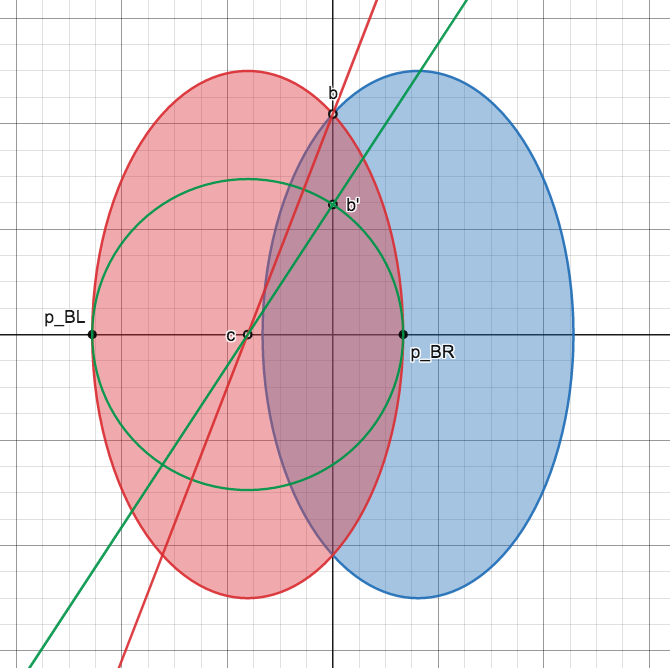
楕円の交点は、2式の y が等しいことから \((x, y) = \left(0, \pm \frac{d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}\right) \) である(このうち正の部分の点を \(b\) としておく)。ここで、上図のように次の条件を持つ円(図内緑円)を考える。
- 円の中心 \(c\) が \(\frac{ p_{\mathrm{BR}}(\theta)+ p_{\mathrm{BL}}(\theta)}{2} \)
- 円の半径が \(\frac{ p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}{2} \)
この真円の面積と、ピンホール後面の楕円の面積比 \(R\) は
\[R = \frac{\text{後面の楕円}}{\text{真円}} = \frac{d}{p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}. \]
求める面積は点 \(b\)、原点 \(O\) 、\(p_{\mathrm{BR}}(\theta)\) が囲う部分の 4 倍である。これを直接求めることはできないので、\(b\) の位置に相当する真円上の点 \(b'\) を求め、面積比 \(R\) をかける。
まず直線 \(\overline{bc}\) の式を求める。
\[ \begin{aligned} \overline{bc} &= \frac{0-\frac{d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}}{\frac{p_{\mathrm{BR}}(\theta) + p_{\mathrm{BL}}(\theta)}{2} - 0} \left( x - \frac{p_{\mathrm{BR}}(\theta) + p_{\mathrm{BL}}(\theta)}{2} \right) \\ &= -\frac{2d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)^2 - p_{\mathrm{BL}}(\theta)^2} \left( x - \frac{p_{\mathrm{BR}}(\theta) + p_{\mathrm{BL}}(\theta)}{2} \right). \end{aligned} \]
よって直線 \(\overline{b'c}\) の式は次の通り:
\[ \overline{b'c} = -\frac{1}{R} \frac{2d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)^2 - p_{\mathrm{BL}}(\theta)^2} \left( x - \frac{p_{\mathrm{BR}}(\theta) + p_{\mathrm{BL}}(\theta)}{2} \right). \]
\(b'c\) の傾きより角度 \(\alpha = \angle'bcO\) が求まるので、扇形 \(\overgroup{b'cp_{\mathrm{BR}}(\theta)}\) の面積 \(A_1\) は:
\[ \begin{aligned} A_1 &= \frac{1}{2}\left( \frac{ p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}{2} \right)^2 \alpha \\ &= \frac{1}{2}\left( \frac{ p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}{2} \right)^2 \tan^{-1} \left( -\frac{1}{R} \frac{2d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)^2 - p_{\mathrm{BL}}(\theta)^2} \right)\\ \end{aligned} \]
三角形 \(\triangle b'cO\) の面積 \(A_2\) は:
\[A_2 = \frac{1}{2} \frac{|p_{\mathrm{BR}}(\theta)+ p_{\mathrm{BL}}(\theta)|}{2} \frac{\frac{d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}}{R} \]
よって求める面積\(A(\theta)\) は:
\[ \begin{aligned} A(\theta) = 4R(A_1 - A_2) &= 4R\left( \frac{1}{2}\left( \frac{ p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}{2} \right)^2 \tan^{-1} \left( -\frac{1}{R} \frac{2d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)^2 - p_{\mathrm{BL}}(\theta)^2} \right) - \frac{1}{2} \frac{|p_{\mathrm{BR}}(\theta)+ p_{\mathrm{BL}}(\theta)|}{2} \frac{\frac{d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}}{R} \right) \\ &= 2R\left( \frac{ p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}{2} \right)^2 \tan^{-1} \left( -\frac{1}{R} \frac{2d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta)^2 - p_{\mathrm{BL}}(\theta)^2} \right) - d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|} \frac{|p_{\mathrm{BR}}(\theta)+ p_{\mathrm{BL}}(\theta)|}{p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)} \\ &= \frac{d}{2}\left( p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta) \right) \tan^{-1} \left( - \frac{2\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|}}{p_{\mathrm{BR}}(\theta) + p_{\mathrm{BL}}(\theta)} \right) - d\sqrt{|p_{\mathrm{BR}}(\theta)p_{\mathrm{BL}}(\theta)|} \frac{|p_{\mathrm{BR}}(\theta)+ p_{\mathrm{BL}}(\theta)|}{p_{\mathrm{BR}}(\theta)- p_{\mathrm{BL}}(\theta)}. \\ \end{aligned} \]
\(p_{\mathrm{BR}}(\theta), p_{\mathrm{BL}}(\theta)\) の式では全体像が掴めないので、 \(p_{\mathrm{BR}}(\theta) - p_{\mathrm{BL}}(\theta),\ \) \(p_{\mathrm{BR}}(\theta) + p_{\mathrm{BL}}(\theta),\ \) \(p_{\mathrm{BR}}(\theta) \cdot p_{\mathrm{BL}}(\theta)\) を三角関数の諸公式を用いて計算すると、
\[ \begin{aligned} p_{\mathrm{BR}}(\theta) - p_{\mathrm{BL}}(\theta) &= d \cos \theta, \\ p_{\mathrm{BR}}(\theta) + p_{\mathrm{BL}}(\theta) &= -t \sin \theta, \\ p_{\mathrm{BR}}(\theta) \cdot p_{\mathrm{BL}}(\theta) &= -\frac{\left(\frac{d}{2} \right)^2 + \left(\frac{t}{2} \right)^2}{2} (\cos 2\theta - \cos 2\Theta) \\ &(\text{where}\ \Theta = \tan ^{-1}(d/t)) \end{aligned} \]
なので、それぞれ代入すると:
\[ A(\theta) = \frac{d^2}{2} \cos \theta \tan ^{-1} \left( \frac{\sqrt{2 \left( \left(\frac{d}{2} \right)^2 + \left(\frac{t}{2} \right)^2 \right) (\cos 2\theta - \cos 2\Theta)}}{ t \sin \theta} \right) - \frac{t}{\sqrt{2}} \tan \theta \sqrt{\left(\frac{d}{2} \right)^2 + \left(\frac{t}{2} \right)^2} \sqrt{\cos 2\theta - \cos 2\Theta}. \]
\(\theta=0\) の時の面積はピンホールの穴の面積と等しいから \(\pi(d/2)^2\) なので、\(\theta\) での明るさの比 \(B(\theta)\) は:
\[B(\theta) = \frac{A(\theta)}{A(0)} = \frac{A(\theta)}{\pi(d/2)^2}. \]
上図は \(d, t\) をそれぞれ独立に動かした時の明るさであるが、見てわかる通り \(d/t\) の比で明るさが決まる。どんなに良い条件でも \(\cos \theta\) (図内点線)以上の明るさにはならない。
コサイン則
ある地点に届く光量は光源との距離の二乗に反比例する。このことから、平像面に届く光量を計算できる。
焦点距離\(f\) の平像面上で中心から \(x\) だけ離れた位置を考える。中心と \(x\) がピンホールでなす角を \(\phi\) とする\((\tan\phi = x/f)\)。
このとき\(x\) に届く光量を \(I(\phi)\) で定めるとき、\(I(\phi) \propto 1/(\text{距離})^2 = 1/(f/\cos\phi)^2.\) また、中央の光量は \(I(0) \propto 1/(f)^2\) であるから、中央部と \(x\) 部分の光量比は、
\[ \begin{aligned} \frac{I(\phi)}{I(0)} &= \frac{1/(f/\cos\phi)^2}{1/(f)^2} \\ &= \cos^2 \phi. \end{aligned} \]
これがコサイン則で、 \(\phi=45\degree\) つまり対角 90°で端は一段暗く、 \(\phi=60\degree\) つまり対角 120°で端は二段暗くなる。もちろんこれは光束の歪みなどを考慮していないから、あわせると \(B(\phi)\cos^2 \phi\) だけ暗くなり、平像面では \(\cos^3 \phi\) 以上隅は明るくならない。
更に詳しい解説は像面上の減光量で考察する。
像のブレ
ピンホール写真をよく見る方はご存知かもしれないが、特に画角の大きなピンホール写真は画面の端で外側に流れるような像のブレが発生する。これはピンホールが外界を形通りに写すのは像面が球面のときだからである。なので平像面上では中央から離れるほど、半径方向にブレが生じるのだ。
ここでは、像が中央にできる場合と、像が \(\phi\) の位置にできる場合の、像の拡大率について考察する。
ここで言う拡大率とは、「角度 k°~(k+1)° がつくる平像面の長さ」「角度 0°~1° がつくる平像面の長さ」の比較である。より正確には、「角度 0°~1° がつくる"平"像面の長さ」ではなく「角度 0°~1° がつくる"円"像面の長さ」である(円像面については後述する)が、この二つはほぼ同じ値であるのであまり重要ではない。式にすると、
\[ \begin{aligned} m(\phi) = \frac{L(\phi+1\degree) - L(\phi)}{L(1\degree) - L(0)} \end{aligned} \]
である。ただし \(L(\phi)\) は像中央からピンホールになす角 \(\phi\) をつくる像面までの長さとする。焦点距離は \(f\) であるから、 \(L(\phi)\) は
\[ \begin{aligned} L(\phi) = f \tan\phi. \end{aligned} \]
よって
\[ \begin{aligned} m(\phi) &= \frac{\tan(\phi+1\degree) - \tan(\phi)}{\tan(1\degree) - \tan(0)} \\ &\approx \frac{\tan(\phi+\pi/180) - \tan(\phi)}{\pi/180-0} \\ &= \frac{180}{\pi}(\tan(\phi+\pi/180) - \tan(\phi)). \end{aligned} \]
ただし角度はラジアンに揃えている。
……とわさわざ正確を喫して計算したが、式の二段目をよく見るとこれは微分の定義2である。実際に関数を重ねてもほぼ等しいことがわかる。
さて、拡大率はというと、
- 29° で 1.3 倍に拡大
- 35° で 1.5 倍に拡大
- 45° で 2 倍に拡大
- 51° で 2.5 倍に拡大
と、像の隅にいくに連れて拡大率は上昇していく。さすがに 2 倍になると実際の写真を見てもはっきりしてくるだろう。
しかし、ある意味ではこの像の流れが写真の味にもなり得る。これを補正しようとするか、そのままでいいとするかはその人次第だ。もちろんそれは周辺光量落ちも同様である。
曲像面
ここまでの考察は全て平面にできる像を考察した(図黒線)。現時点ではデジタルの場合は上記の話で十分である。しかしフィルムの利点として、像面をある程度自由に変化させられる点が挙げられる。
まず思い付くのが、ピンホールから像までの距離が常に等しい曲面である。このページでは便宜上「円像面」と呼ぶことにする(図赤線)。後述するが、円像面の利点は横方向の像のブレが無いことである。また、周辺光量落ちも平像面と比べると少なく、広い画角を得るのに必要な像面が平像面より短くて済む。このため、ondu ondurama 6x17 や realitysosubtle 6x17 などのパノラマピンホールカメラが円像面を採用している。円像面の欠点は中央線以外の水平線が曲がることで、この種類のピンホールカメラは水平レベルを出すことで無限遠を中央線に合わせて水平にしている。
また、ここで新たに計算したのだが、周辺光量落ちを補正するような曲面を考えた(図紫線)。円像面より更に像面を内側に曲げることで、横方向で光量がほぼ一定となる。ここでは便宜上「等光像面」と名付けた。円像面と同様、中央線以外の水平線が曲がってしまう。
ここでは平像面・円像面・等光像面について、角度 \(\phi\) の位置での光量・像面の長さ・像の縮小拡大率などについて考察する。
これ以降で用いる式は以下の通りである。
- ピンホール … 原点 \(O(0, 0)\)
- 中央部の光量(全像面共通) … \(I(0)\propto 1/f^2\)
- 平像面 … \(x=f\)
- 円像面 … \(x^2+y^2=f^2, r(\phi) = f\)
- 等光像面 … \(x ^{4/3}+\frac{y^2}{x ^{2/3}}=f ^{4/3}, r(\phi) = f\sqrt{\cos\phi}\)
光量
平像面
コサイン則で計算した通り、距離による光量比は \(\cos^2 \phi\) であり、ケラレや光束についても考慮に加えると \(\cos^3 \phi\) である。
円像面
計算するまでもないが、距離による光量比は \(I(\phi) \propto 1/f^2\) より \(I(\phi)/I(0) = 1.\) ケラレや光束についても考慮に加えると \(\cos \phi\) である。平像面と比べると、全領域で光量が増加していることがわかる。
等光像面
円像面より、\(I(\phi)/I(0) = 1/\cos\phi\) となっていれば、ケラレや光束について考慮に加えると光量比は全域で 1 倍となる。このことから逆算して、 \(I(\phi) \propto 1/f^2\cos\phi = 1/(f\sqrt{\cos\phi})^2\) より、ピンホールからの距離の関数 \(r(\phi) = f\sqrt{\cos\phi}\) が求まる(極座標表示)。
パラメータ表示すると
\[ \begin{dcases} x(t) = f \sqrt{\cos t} \,\cos t \\ y(t) = f \sqrt{\cos t} \,\sin t \end{dcases} \]
より変形して
\[ \begin{aligned} x^{4/3}+\frac{y^2}{x^{2/3}}=f^{4/3} \end{aligned} \]
も求まる。
像面の長さ \(L\) と拡大率
計算の前提知識として、曲線の長さの求め方はここを参照してほしい。いづれの方法にせよ、この関数と x 軸が囲む面積が求める曲線の長さである。ただし、ここでいう長さとは像面の中心から対角線の端までの長さを言う。
平像面
これは計算せずとも \(y(\Phi) = l/2\) の長さがすなわちそれである。だがここでは他の条件と同じように計算してこの結果が得られるかどうかを確かめよう。
\(x, y\) をパラメータ表示すると
\[ \begin{dcases} x(t) = f \\ y(t) = f \tan t \end{dcases} \]
であるから、
\[ \begin{dcases} \vphantom{\int}\frac{\partial x}{\partial t} = 0 \\ \frac{\partial y}{\partial t} = f/\cos^2t. \end{dcases} \]
よって求める \(L\) は
\[ \begin{aligned} L &= \int_ {0}^ {\Phi} \sqrt{0^2 + \left( \frac{f}{\cos^2t} \right)^2} \,\mathrm{d}t \\ &= \int_ {0}^ {\Phi} \left| \frac{f}{\cos^2t}\right| \,\mathrm{d}t \\ &= \Bigl[ f\tan t \Bigr] _{0} ^{\Phi} \quad (\because \Phi \le \pi/2) \\ &= f \tan \Phi \\ &= y(\Phi) = l/2. \end{aligned} \]
拡大率は像のブレで考察した通りである。
円像面
これも円の弧長の公式を用いれば \(L = f\Phi\) であるのだが、計算してみる。
\(x, y\) をパラメータ表示すると
\[ \begin{dcases} x(t) = f \cos t \\ y(t) = f \sin t \end{dcases} \]
であるから、
\[ \begin{dcases} \vphantom{\int}\frac{\partial x}{\partial t} = -f \sin t \\ \frac{\partial y}{\partial t} = f \cos t. \end{dcases} \]
よって求める \(L\) は
\[ \begin{aligned} L &= \int_ {0}^ {\Phi} \sqrt{\left( -f \sin t \right)^2 + \left( f \cos t \right)^2} \,\mathrm{d}t \\ &= \int_ {0}^ {\Phi} f \,\mathrm{d}t \\ &= \Bigl[ ft \Bigr] _{0} ^{\Phi} \\ &= f \Phi. \end{aligned} \]
拡大率は、常にピンホールから等距離にあることから常に 1 倍である。
等光像面
\(x, y\) をパラメータ表示してもよいが、式の簡単のため極座標形式を用いる。
\[ \begin{dcases} r(\phi) &= f\sqrt{\cos \phi} \\ \frac{\partial r}{\partial \phi} &= f\frac{-\sin\phi}{2\sqrt{\cos\phi}} \end{dcases} \]
より求める \(L\) は
\[ \begin{aligned} L &= \int _{0} ^{\Phi} \sqrt{\left( r(\phi) \right)^2 + \left( \frac{\partial r}{\partial \phi} \right)^2} \,\mathrm{d}\phi \\ &= \int _{0} ^{\Phi} \sqrt{\left( f\sqrt{\cos\phi} \right)^2 + \left( f\frac{-\sin\phi}{2\sqrt{\cos\phi}} \right)^2} \,\mathrm{d}\phi \\ &= f\int _{0} ^{\Phi} \sqrt{ \cos\phi + \frac{\sin^2\phi}{4\cos\phi} } \,\mathrm{d}\phi \\ &= f\int _{0} ^{\Phi} \sqrt{ \frac{1+3\cos\phi}{4\cos\phi} } \,\mathrm{d}\phi \end{aligned} \]
……とここまでは調子よく行くのだが、これから先は代数的に計算できない(少なくとも手計算と wolframalpha では)。なので代数的に解くのではなく数値計算で求める \(L\) を計測してみようと思う。 (後ほど気付いたが wolframalpha に実際の角度を積分範囲として計算すると実際の数値が得られた。)
積分計算のアルゴリズムはシンプソン法を用いた。
| deg | f(phi) | L |
|---|---|---|
| 0 | 1 | 0 |
| 10 | 0.99622411 | 0.17419738 |
| 20 | 0.98529889 | 0.34691462 |
| 30 | 0.96860425 | 0.51704588 |
| 40 | 0.94914970 | 0.68389873 |
| 50 | 0.93328541 | 0.84765302 |
| 60 | 0.93541435 | 1.0104184 |
| 70 | 0.99371334 | 1.1791788 |
| 80 | 1.2529680 | 1.3775449 |
この表では一部のデータのみを取り出して示しているが、実際には 1° 間隔で計算した。元の関数の曲率も小さいため、 1° という大きめの区切りでも十分(有効 3 桁程度)に精度が出たと判断した。
以下の図は平像面・円像面・等光像面の画角と像の長さをプロットしたものである。それぞれ紫・緑・黄線で示した。ただし等光像面のもの(黄線)は以下の関数で近似したものである。
\[ L(\phi)\approx p(\phi) = \begin{cases} f\left( \frac{1}{3} a_1|\phi|^3+ \frac12 b_1|\phi|^2+c_1|\phi|\right) &(0\le \phi\le 50\pi/180) \\ f\left( \frac{a_2}{2}|\phi|^2 + b_2|\phi| +c_2 \tan(|\phi| - d_2) +e_2 \right) &(50\pi/180\le \phi \lt \pi/2) \end{cases} \]
\[ \begin{aligned} a_1 &=-0.0431259,& b_1 &=-0.0443389,& c_1 &=1.00397. & \\ a_2 &=-0.143677,& b_2 &=0.988301,& c_2 &=0.0352649,& \\ d_2 &=0.106483,& e_2 &=0.0080105.&&& \end{aligned} \]
図より円像面と等光像面の像の長さは大きく異ならないことがわかる。便宜上円像面の像の長さを等光像面のものとして用いて問題ないかもしれない。
また、像のブレでも考察した通り、 \(L(\phi)\) の \(\phi\) での微分(つまり像の微少長さ)こそが拡大率であった。等光像面は 55° 付近では半径方向に約 93% の像の縮小が起こり、 70° 以降は像の拡大が始まる。しかしこれは平像面の拡大と比べると無視できる程度のものであり、実用では意図して像を観察しない限りは気付かない程度の歪みであると考えられる。
以前の近似式(後半を改めた)
\[ \begin{aligned} L(\phi)\approx p(\phi) = \begin{dcases} f\left(\frac13 a_1|\phi|^3+ \frac12 b_1|\phi|^2+c_1|\phi|\right) \ \ \ \ \ &(0\le \phi\le 50\pi/180) \\ f\left(\left.a_2 ^{|\phi|+b_2}\right/\ln\left(a_2\right) + c_2|\phi| + d_2\right) \ \ \ &(50\pi/180\le \phi\lt \pi/2) \end{dcases} \end{aligned} \]
\[ \begin{aligned} a_1 &=-0.0431259,& b_1 &=-0.0443389,& c_1 &=1.00397. & \\ a_2 &=15124.1,& b_2 &=-1.51116,& c_2 &=0.927502,& d_2 =0.039781. \end{aligned} \]
直線像の歪み
平面の格子模様の風景を、各像面のピンホールカメラで捉える場合を考える。
以下の議論で注意してほしい点を挙げる。 像面の長さで行った考察での \((x, y)\)
はそれぞれピンホールから像面中心への奥行き方向とそれに直交する方向であった。
それに対し、ある像面 \(\Pi(x, y)\)
という場合、像面を平面に展開したときの、像面のある位置を表すための座標である。 \(\Pi(x, y)\)
はそれぞれの方向の角度 \(\phi, \psi\)
で定めることができ、そのときは像面の長さを関数とする。つまり\(\Pi(L_x(\phi),
L_y(\psi))\) である (ただし像の曲がり具合によって、関数 \(L_x, L_y\)
はそれぞれ異なることがある)。
この二つの座標系を混同していると計算できないため、注意する必要がある。
平像面
風景面 \(\Pi_o\), ピンホール面、平像面 \(\Pi_ {\mathrm{flat}}\) をぞれぞれ平行に置く。風景面 \(\Pi_o\) 上の座標は \(\Pi_o(X, Y)\) で与え、 \((X, Y) = (0, 0)\) からピンホールまでの距離は \(Z\) である。
平像面 \(\Pi_ \mathrm{flat}\) 上の座標は \(\Pi_ \mathrm{flat}(x, y)\) で与え、 \(\Pi_ \mathrm{flat}(x, y) = (0, 0)\) からピンホールまでの距離は \(f\) (焦点距離)である。ただし \(\Pi_ \mathrm{flat}(x, y)\) の方向は \(\Pi_o(X, Y)\) とは逆方向に定める。これはピンホールを通してできる像は倒立するから、考察のしやすさの為にそうした。
まずは極座標への変換を行う。 \(\Pi_ \mathrm{flat}(x, y)\) の各方向へ、ピンホールになす角を \((\phi, \psi)\) とすると、 \(\Pi_ \mathrm{flat}(f\tan\phi, f\tan\psi)\) と表せる。同様にして \(\Pi_o(Z\tan\phi, Z\tan\psi)\) と表せる (光は直進するためなす角は同じ)。
\(\Pi_o(X, Y)\) からピンホールまでの距離を \(K(\phi, \psi)\), \(\Pi_ \mathrm{flat}(x, y)\) からピンホールまでの距離を \(k(\phi, \psi)\) で表すとすると、
\[ \begin{aligned} K(\phi, \psi) &= \frac{Z}{\cos\phi \ \cos\psi}, \\ k(\phi, \psi) &= \frac{f}{\cos\phi \ \cos\psi}. \end{aligned} \]
\(\Pi_o(X, Y)\) にある十分小さな物体 \(\Delta A\) が、平像面 \(\Pi_ \mathrm{flat}(x, y)\) 上につくる像 \(\Delta a\) の比は、 \(K(\phi, \psi)\) と \(k(\phi, \psi)\) の比と等しい。よって、
\[ \begin{aligned} \frac{\Delta A}{\Delta a} &= \frac{K(\phi, \psi)}{k(\phi, \psi)} \\ &= \frac{Z}{f}. \\ \therefore \Delta a &= \frac{f}{Z}\Delta A. \end{aligned} \]
よって平像面全域において、対象物の大きさと距離が同じなら、同じ大きさで像は写る。
円像面
平像面での議論を踏まえ、ここでは円像面 \(\Pi_ {\mathrm{circular}}\) を置く。風景面 \(\Pi_o\) はそのまま用いる。
極座標系で表現すると、 \(\Pi_ {\mathrm{circular}}(f\phi, f\tan\psi)\) とできる (平面をそのまま曲げられるのは一軸方向(今回は\(x\)軸方向)のみなので、\(y\)軸は平像面と同じ話になる)。
このときピンホールから \(\Pi_ {\mathrm{circular}}\) までの距離は、
\[ \begin{aligned} k(\phi, \psi) &= \frac{f}{\cos\psi}. \end{aligned} \]
よって、
\[ \begin{aligned} \frac{\Delta A}{\Delta a} &= \frac{K(\phi, \psi)}{k(\phi, \psi)} \\ &= \frac{Z}{f \cos\phi} \\ \therefore \Delta a &= \frac{f}{Z}\Delta A\cos\phi. \end{aligned} \]
\(\cos\phi \le 1\ (0\le\phi\le\pi/2)\) であるから、平像面と比較すると小さな像が周辺部で得られることがわかる。
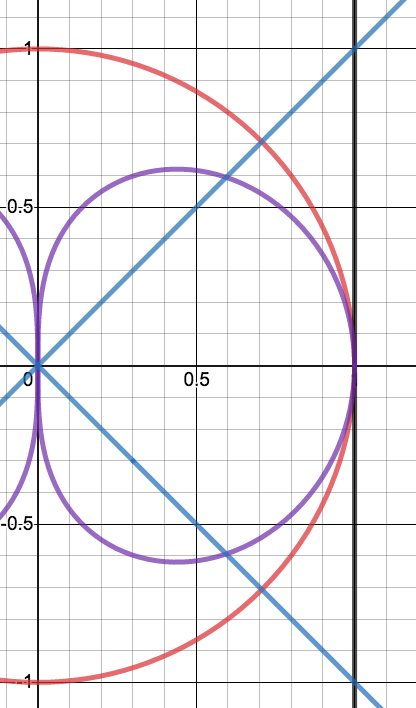
下のグラフは、平像の時と同じ格子を円像で捉えたものである(像の縦横比は長さで実寸比)。平像では黒線で示した 1 [mm] 格子が、円像では紫線で示すように歪む(金線は 0.5 [mm] の補線)。平像では\(x\)軸方向に十分長い像面が必要となるが、円像では比較的短い像面で広い画角をカバーすることができる。
等光像面
平像面での議論を踏まえ、ここでは等光像面 \(\Pi_ {\mathrm{panlight}}\) を置く。風景面 \(\Pi_o\) はそのまま用いる。
極座標系で表現すると、 \(\Pi_ {\mathrm{panlight}}(p(\phi), f\tan\psi)\) とできる (\(p(\phi)\)はここで求めた)。
このときピンホールから \(\Pi_ {\mathrm{panlight}}\) までの距離は、
\[ \begin{aligned} k(\phi, \psi) &= \frac{f\sqrt{\cos\phi}}{\cos\psi}. \end{aligned} \]
よって、
\[ \begin{aligned} \frac{\Delta A}{\Delta a} &= \frac{K(\phi, \psi)}{k(\phi, \psi)} \\ \therefore \Delta a &= \frac{f}{Z}\Delta A\cos ^{3/2}\phi. \end{aligned} \]
下のグラフは、平像の時と同じ格子を等光像で捉えたものである(像の縦横比は長さで実寸比)。円像と同様に、平像では黒線で示した 1 [mm] 格子が、等光像では緑線で示すように歪む(金線は 0.5 [mm] の補線)。左右の端では特に円像より強く歪むことが分かる。円像と同様に、比較的短い像面で広い画角をカバーすることができる上に、端での光量落ちを補償する曲像である。
なお、図 9 の作図において \(x=p(\phi)\) の逆関数 \(\phi = p
^{-1}(x)\) が必要であったので、これも \(p(\phi)\) を求めた時と同様に
gnuplot の近似機能で求めた。
この図をよく見ると、 \(\phi=0°\) での\(y\)の値が 5.5–6 [mm]
程度の(画面外にある)曲線が、 \(\phi=70°\)
では画面内に収まる位置に到達するほど歪んでいる。
虞らく \((x, y) = (1.2, 1.1)\) の位置はピンホールが像中央 \((0, 0)\)
となす角が \(\theta=80°\)
以上あると思われ、その範囲はピンホールの設計が十分広角でないとカバーできない。
像面上の減光量
このセクションでは、各像面のどの位置でどれほどの減光が起こるのかを考察する。
周辺光量落ちで考察した通り、像の減光には「ピンホールからの距離」「ピンホールへの光の入射角
+
ピンホールの厚みによる開口の変形」が関わっていた。しかし「ピンホールの厚みによる開口の変形」を考慮に入れると計算が不必要に複雑になることが考えられるため、ここでは「ピンホールからの距離」と「ピンホールへの光の入射角による開口の変形」のみで計算することにする。これは、ピンホールの厚みがピンホールの直径と比べて十分小さい場合
\((t \ll d)\) の減光を考えることと等しいと言える。
まずは、像面中心部の光量と任意の位置の光量の比 \(I(\theta)/I(0)\)
を、写真で用いられる減光量 \(S\) に変換することを考える。
明らかに言えることは、光量比 \(I(\theta)/I(0)=0.5\) のとき -1 段(stop)の減光、
\(I(\theta)/I(0)=0.25\) のとき -2 段、というようになっているということだ。
これより、
\[ I(\theta) = I(0) \times 2 ^{S\mathrm{ \ stop(s)}} \]
であるから、例えば -1/3 段の減光は光量比 \(2 ^{-1/3} \approx 0.7937\) 倍である。上の式を変形して、
\[ \begin{aligned} I(\theta)/I(0) &= 2 ^S \\ S &= \log _2 \frac{I(\theta)}{I(0)}. \end{aligned} \]
次に、直線像の歪みで用いた \((\phi, \psi)\) という位置指標から、像面中心からピンホールになす角 \(\theta\) への変換を考える必要がある。
平像面
理想的なピンホールで、位置 \(x\) における光量比 \(B(\theta) \cos ^2\theta\) は \( \cos^3 (\phi), \ \phi =\tan ^{-1}(x/f)\) だから、
\[ S = \log _2 \left( \cos ^3 \left( \tan ^{-1} \left( \frac{x}{f} \right)\right)\right) \\ x = f \tan(\cos ^{-1}(\sqrt[3]{2^S})). \]
いくつかのピンホールカメラで計算したところ、像面の端はどれも -4 段ほどになっている。自作の際には目安になるだろう。
またピンホールの厚みが無視できない場合は、正確に求めるには繁雑な計算をする必要があるのだが、ここでは \(S = -6.5 [\mathrm{stops}]\) 程度なら近似できる係数をたまたま見つけたので紹介する。ピンホール直径 \(d\)、厚さ \(t\) の減光 \(S_\mathrm{thick}\) は:
\[ \begin{aligned} S_\mathrm{thick} &= 2 ^{2t/d} S \\ &= 2 ^{2t/d} \log _2 \left( \cos ^3 \left( \tan ^{-1} \left( \frac{x}{f} \right)\right)\right). \end{aligned} \]
脚注:
実際にはこの \(\sqrt{2.44}\approx1.562\) の値には幾つかの論争があり、情報として良くまとまっているのがここである。シャープネスが最適である場合よりもコントラストが最適であるほうが人の目には尖鋭に「見える」という話も含まれていた。個人的には、 \(M=0.01 – 0.0001\) 程度に収まる被写体が多いことも考えると、1.55–1.56 程度が最適であると考えている。
微分の定義は以下の通り。 \(h\) を \(\pi/180\) に、 \(f(x)\) を \(\tan(\phi)\) すると当該の式となる。 \[ \begin{aligned} f'(x) =\lim _{h\rightarrow0}\frac{f(x+h) - f(x)}{h}. \end{aligned} \] \(\tan x\) の微分は \(1/\cos ^2 x\) なので、これに求めたい角度を適応するとその角度での像の流れ方が分かる。